$$\eta$$ scaling for dynamical nhyp

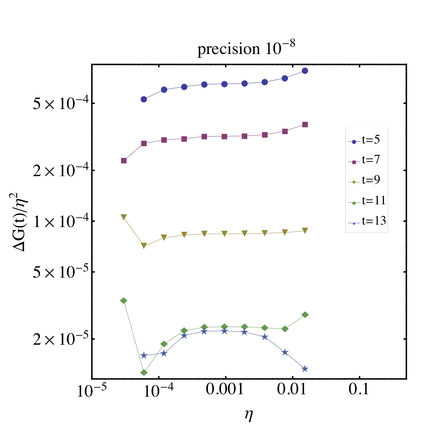
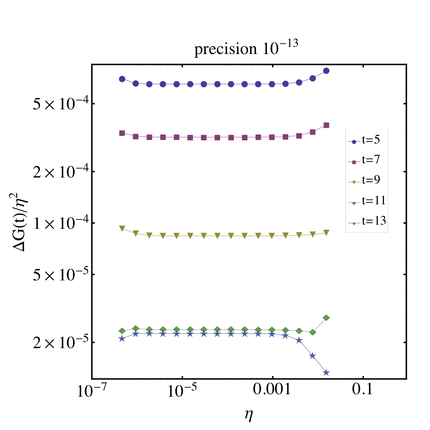
We performed a scaling test of the $\eta$ parameter on a single $24^3 \times48$ nhyp dynamical lattice. We want to determine a regime of $\eta$ values where the $\eta^2$ scaling of the mass shift is valid. As we go to smaller values of $\eta$ numerical limitations will begin to arise. We want to find where this break down occurs. We did the analysis for 2 different precisions for the CG inverter: $10^{-8}$ and $10^{-13}$.

For the $10^{-8}$ precision we ran the simulation for 10 values of $\eta$ starting from $\eta_0 = 3.0\times 10^{-5}$. The subsequent values of $\eta$ are in powers of 2, i.e. $\eta_1 = 2^1 \eta_0$, $\eta_2 = 2^2 \eta_0$ etc. For the $10^{-13}$ precision we ran the simulation for 16 values of $\eta$ starting from $\eta_0 = 4.6875\times 10^{-7}$. This value is chosen such that $2^7( 4.6875\times 10^{-7}) = 3.0\times 10^{-5}$.

We plot $(G_E(t) -G_0(t))/\eta^2$ as a function of $\eta$. We expect a constant behavior in the region where the $\eta^2$ scaling is valid. The plot on the right shows our results for neutron at several different time slices. We also list the parameters used in this analysis in the table below.

Configuration

knhyp242448_beta7.1_kappa0.1282_023

ran on Fermilab with 4 GPUs

CG precision	1e-8	1e-13
$\kappa$	0.1282	0.1282
n iterations	1030	1250
timing for 1 inversion ~	18 sec	22 sec

Plots